Open
Description
状态转移方程
定义 dp[i][j]:以坐标 (i,j) 为右下角的最大正方形边长。
-
(i,j) 为 0 时,无法构成正方形,
dp[i][j] = 0 -
(i,j) 为 1 时,
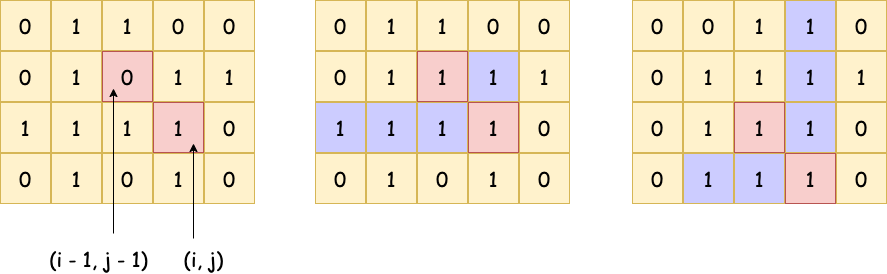
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1
一个正方形的最大边长决定于它左方、上方、斜上方的位置所能形成的最大正方形的边长,即:三者的最小值 + 自身的长度 1。
如图:紫色部分代表不断向左、上方尝试。
为了避免边界条件判断,可以将 dp 数组的长和宽都增加 1。
const maximalSquare = function(matrix) {
if (!matrix.length) return 0
const dp = new Array(matrix.length + 1).fill(0).map(() => new Array(matrix[0].length + 1).fill(0))
let maxLen = 0
for (let i = 1; i < dp.length; i++) {
for (let j = 1; j < dp[0].length; j++) {
if (matrix[i - 1][j - 1] === '1') {
dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]) + 1
maxLen = Math.max(dp[i][j], maxLen)
}
}
}
return maxLen * maxLen
}- 时间复杂度: O(m * n)
- 空间复杂度: O(m * n)