Skip to content

Commit 334853a

Browse files
tcdtisttcdtist
committed
chore(translate): add Vietnamese
1 parent 7d12132 commit 334853a

File tree

23 files changed

+755
-277
lines changed

23 files changed

+755
-277
lines changed

‎src/algorithms/search/jump-search/README.md

+2-2
Original file line numberDiff line numberDiff line change
@@ -1,7 +1,7 @@
11
# Tìm Kiếm Bước Nhảy
22

3-
_Tiếp tục đọc trong các ngôn ngữ khác:_
4-
[_Tiếng Việt_](README.md)
3+
_Nhấn vào đây để đọc bằng ngôn ngữ khác:_
4+
[_English_](README.en-EN.md)
55

66
Giống như Tìm kiếm nhị phân, **Tìm kiếm bước nhảy** (hoặc **Tìm kiếm khối**) là một thuật toán tìm kiếm
77
cho các mảng đã được sắp xếp. Ý tưởng cơ bản là kiểm tra ít phần tử hơn

‎src/algorithms/search/linear-search/README.md

+2-2
Original file line numberDiff line numberDiff line change
@@ -1,7 +1,7 @@
11
# Tìm Kiếm Tuyến Tính
22

3-
_Tiếp tục đọc trong các ngôn ngữ khác:_
4-
[_Tiếng Việt_](README.md)
3+
_Nhấn vào đây để đọc bằng ngôn ngữ khác:_
4+
[_English_](README.en-EN.md)
55

66
Trong khoa học máy tính, tìm kiếm tuyến tính hoặc tìm kiếm tuần tự là một
77
phương pháp để tìm một giá trị mục tiêu trong một danh sách. Nó kiểm tra

‎src/algorithms/sets/cartesian-product/README.md

+11-8
Original file line numberDiff line numberDiff line change
@@ -1,14 +1,17 @@
1-
# Cartesian Product
1+
# Cartesian Product - Tích Descartes
22

3-
In set theory a Cartesian product is a mathematical operation that returns a set
4-
(or product set or simply product) from multiple sets. That is, for sets A and B,
5-
the Cartesian product A × B is the set of all ordered pairs (a, b)
6-
where a ∈ A and b ∈ B.
3+
_Nhấn vào đây để đọc bằng ngôn ngữ khác:_
4+
[_English_](README.en-EN.md)
75

8-
Cartesian product `AxB` of two sets `A={x,y,z}` and `B={1,2,3}`
6+
Trong lý thuyết tập hợp, tích Descartes là một phép toán toán học trả về một tập hợp
7+
(hoặc tập hợp tích hoặc đơn giản là tích) từ nhiều tập hợp. Đó là, đối với các tập hợp A và B,
8+
tích Descartes A × B là tập hợp của tất cả các c��p có thứ tự (a, b)
9+
trong đó a ∈ A và b ∈ B.
910

10-
![Cartesian Product of Two Sets](https://upload.wikimedia.org/wikipedia/commons/4/4e/Cartesian_Product_qtl1.svg)
11+
Tích Descartes `AxB` của hai tập hợp `A={x,y,z}` và `B={1,2,3}`
1112

12-
## References
13+
![Tích Descartes của Hai Tập Hợp](https://upload.wikimedia.org/wikipedia/commons/4/4e/Cartesian_Product_qtl1.svg)
14+
15+
## Tham Khảo
1316

1417
[Wikipedia](https://en.wikipedia.org/wiki/Cartesian_product)

‎src/algorithms/sets/combination-sum/README.en-EN.md

+61
Original file line numberDiff line numberDiff line change
@@ -1,2 +1,63 @@
1+
# Combination Sum Problem
2+
13
_Read this in other languages:_
24
[_Tiếng Việt_](README.md)
5+
6+
Given a **set** of candidate numbers (`candidates`) **(without duplicates)** and
7+
a target number (`target`), find all unique combinations in `candidates` where
8+
the candidate numbers sums to `target`.
9+
10+
The **same** repeated number may be chosen from `candidates` unlimited number
11+
of times.
12+
13+
**Note:**
14+
15+
- All numbers (including `target`) will be positive integers.
16+
- The solution set must not contain duplicate combinations.
17+
18+
## Examples
19+
20+
```
21+
Input: candidates = [2,3,6,7], target = 7,
22+
23+
A solution set is:
24+
[
25+
[7],
26+
[2,2,3]
27+
]
28+
```
29+
30+
```
31+
Input: candidates = [2,3,5], target = 8,
32+
33+
A solution set is:
34+
[
35+
[2,2,2,2],
36+
[2,3,3],
37+
[3,5]
38+
]
39+
```
40+
41+
## Explanations
42+
43+
Since the problem is to get all the possible results, not the best or the
44+
number of result, thus we don’t need to consider DP (dynamic programming),
45+
backtracking approach using recursion is needed to handle it.
46+
47+
Here is an example of decision tree for the situation when `candidates = [2, 3]` and `target = 6`:
48+
49+
```
50+
0
51+
/ \
52+
+2 +3
53+
/ \ \
54+
+2 +3 +3
55+
/ \ / \ \
56+
+2 ✘ ✘ ✘ ✓
57+
/ \
58+
✓ ✘
59+
```
60+
61+
## References
62+
63+
- [LeetCode](https://leetcode.com/problems/combination-sum/description/)

‎src/algorithms/sets/combination-sum/README.md

+17-19
Original file line numberDiff line numberDiff line change
@@ -1,23 +1,23 @@
1-
# Combination Sum Problem
1+
# Combination Sum Problem - Vấn đề Tổ hợp Tổng
22

3-
Given a **set** of candidate numbers (`candidates`) **(without duplicates)** and
4-
a target number (`target`), find all unique combinations in `candidates` where
5-
the candidate numbers sums to `target`.
3+
_Đọc bản dịch này bằng các ngôn ngữ khác:_
4+
[_English_](README.en-EN.md)
65

7-
The **same** repeated number may be chosen from `candidates` unlimited number
8-
of times.
6+
Cho một **tập hợp** các số ứng viên (`candidates`) **(không có phần tử trùng lặp)** và một số mục tiêu (`target`), hãy tìm tất cả các tổ hợp duy nhất trong `candidates` sao cho tổng các số ứng viên bằng `target`.
97

10-
**Note:**
8+
**Cùng** một số lặp lại có thể được chọn từ `candidates` không giới hạn lần.
119

12-
- All numbers (including `target`) will be positive integers.
13-
- The solution set must not contain duplicate combinations.
10+
**Ghi chú:**
1411

15-
## Examples
12+
- Tất cả các số (bao gồm cả `target`) sẽ là các số nguyên dương.
13+
- Tập hợp giải pháp không được chứa các tổ hợp trùng lặp.
14+
15+
## Ví dụ
1616

1717
```
1818
Input: candidates = [2,3,6,7], target = 7,
1919
20-
A solution set is:
20+
Một tập hợp giải pháp là:
2121
[
2222
[7],
2323
[2,2,3]
@@ -27,21 +27,19 @@ A solution set is:
2727
```
2828
Input: candidates = [2,3,5], target = 8,
2929
30-
A solution set is:
30+
Một tập hợp giải pháp là:
3131
[
3232
[2,2,2,2],
3333
[2,3,3],
3434
[3,5]
3535
]
3636
```
3737

38-
## Explanations
38+
## Giải thích
3939

40-
Since the problem is to get all the possible results, not the best or the
41-
number of result, thus we don’t need to consider DP (dynamic programming),
42-
backtracking approach using recursion is needed to handle it.
40+
Vì vấn đề là lấy tất cả các kết quả có thể, không phải là tốt nhất hoặc số lượng kết quả, do đó chúng ta không cần xem xét DP (programing dynamic), cần sử dụng phương pháp backtracking sử dụng đệ quy để xử lý nó.
4341

44-
Here is an example of decision tree for the situation when `candidates = [2, 3]` and `target = 6`:
42+
Dưới đây là một ví dụ về cây quyết định cho tình huống khi `candidates = [2, 3]` và `target = 6`:
4543

4644
```
4745
0
@@ -52,9 +50,9 @@ Here is an example of decision tree for the situation when `candidates = [2, 3]`
5250
/ \ / \ \
5351
+2 ✘ ✘ ✘ ✓
5452
/ \
55-
✓ ✘
53+
✓ ✘
5654
```
5755

58-
## References
56+
## Tài liệu tham khảo
5957

6058
- [LeetCode](https://leetcode.com/problems/combination-sum/description/)

‎src/algorithms/sets/combinations/README.en-EN.md

+69
Original file line numberDiff line numberDiff line change
@@ -1,2 +1,71 @@
1+
# Combinations
2+
13
_Read this in other languages:_
24
[_Tiếng Việt_](README.md)
5+
6+
When the order doesn't matter, it is a **Combination**.
7+
8+
When the order **does** matter it is a **Permutation**.
9+
10+
**"My fruit salad is a combination of apples, grapes and bananas"**
11+
We don't care what order the fruits are in, they could also be
12+
"bananas, grapes and apples" or "grapes, apples and bananas",
13+
its the same fruit salad.
14+
15+
## Combinations without repetitions
16+
17+
This is how lotteries work. The numbers are drawn one at a
18+
time, and if we have the lucky numbers (no matter what order)
19+
we win!
20+
21+
No Repetition: such as lottery numbers `(2,14,15,27,30,33)`
22+
23+
**Number of combinations**
24+
25+
![Formula](https://www.mathsisfun.com/combinatorics/images/combinations-no-repeat.png)
26+
27+
where `n` is the number of things to choose from, and we choose `r` of them,
28+
no repetition, order doesn't matter.
29+
30+
It is often called "n choose r" (such as "16 choose 3"). And is also known as the Binomial Coefficient.
31+
32+
## Combinations with repetitions
33+
34+
Repetition is Allowed: such as coins in your pocket `(5,5,5,10,10)`
35+
36+
Or let us say there are five flavours of ice cream:
37+
`banana`, `chocolate`, `lemon`, `strawberry` and `vanilla`.
38+
39+
We can have three scoops. How many variations will there be?
40+
41+
Let's use letters for the flavours: `{b, c, l, s, v}`.
42+
Example selections include:
43+
44+
- `{c, c, c}` (3 scoops of chocolate)
45+
- `{b, l, v}` (one each of banana, lemon and vanilla)
46+
- `{b, v, v}` (one of banana, two of vanilla)
47+
48+
**Number of combinations**
49+
50+
![Formula](https://www.mathsisfun.com/combinatorics/images/combinations-repeat.gif)
51+
52+
Where `n` is the number of things to choose from, and we
53+
choose `r` of them. Repetition allowed,
54+
order doesn't matter.
55+
56+
## Cheatsheet
57+
58+
![Permutations and Combinations Overview](./images/overview.png)
59+
60+
![Combinations overview](./images/combinations-overview.jpg)
61+
62+
| | |
63+
| --------------------------------------------------------------------------- | --------------------------------------------------------------------------------- |
64+
| ![Combinations with repetition](./images/combinations-with-repetitions.jpg) | ![Combinations without repetition](./images/combinations-without-repetitions.jpg) |
65+
66+
_Made with [okso.app](https://okso.app)_
67+
68+
## References
69+
70+
- [Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
71+
- [Permutations/combinations cheat sheets](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)

‎src/algorithms/sets/combinations/README.md

+44-41
Original file line numberDiff line numberDiff line change
@@ -1,68 +1,71 @@
1-
# Combinations
1+
# Combinations - Tổ Hợp
22

3-
When the order doesn't matter, it is a **Combination**.
3+
_Đọc bản dịch này bằng các ngôn ngữ khác:_
4+
[_English_](README.en-EN.md)
45

5-
When the order **does** matter it is a **Permutation**.
6+
Khi thứ tự không quan trọng, đó là **Tổ hợp**.
67

7-
**"My fruit salad is a combination of apples, grapes and bananas"**
8-
We don't care what order the fruits are in, they could also be
9-
"bananas, grapes and apples" or "grapes, apples and bananas",
10-
its the same fruit salad.
8+
Khi thứ tự **quan trọng** thì đó là **Hoán vị**.
119

12-
## Combinations without repetitions
10+
**"Món tráng miệng của tôi là một tổ hợp của táo, nho và chuối"**
11+
Chúng tôi không quan tâm thứ tự của các loại trái cây, chúng cũng có thể là
12+
"chuối, nho và táo" hoặc "nho, táo và chuối",
13+
đó là một món tráng miệng giống nhau.
1314

14-
This is how lotteries work. The numbers are drawn one at a
15-
time, and if we have the lucky numbers (no matter what order)
16-
we win!
15+
## Tổ hợp không lặp lại
1716

18-
No Repetition: such as lottery numbers `(2,14,15,27,30,33)`
17+
Đây là cách làm việc của các trò chơi xổ số. Các số được rút ra một cách
18+
lần lượt, và nếu chúng ta có các số may mắn (bất kể thứ tự)
19+
thì chúng ta sẽ chiến thắng!
1920

20-
**Number of combinations**
21+
Không Lặp Lại: chẳng hạn như các số xổ số `(2,14,15,27,30,33)`
2122

22-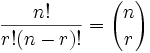
![Formula](https://www.mathsisfun.com/combinatorics/images/combinations-no-repeat.png)
23+
**Số lượng tổ hợp**
2324

24-
where `n` is the number of things to choose from, and we choose `r` of them,
25-
no repetition, order doesn't matter.
25+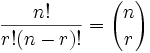
![Công thức](https://www.mathsisfun.com/combinatorics/images/combinations-no-repeat.png)
2626

27-
It is often called "n choose r" (such as "16 choose 3"). And is also known as the Binomial Coefficient.
27+
trong đó `n` là số lượng thứ cần chọn từ, và chúng ta chọn `r` trong số đó,
28+
không lặp lại, thứ tự không quan trọng.
2829

29-
## Combinations with repetitions
30+
Nó thường được gọi là "n chọn r" (như "16 chọn 3"). Và còn được gọi là Hệ số Nhị thức.
3031

31-
Repetition is Allowed: such as coins in your pocket `(5,5,5,10,10)`
32+
## Tổ hợp có lặp lại
3233

33-
Or let us say there are five flavours of ice cream:
34-
`banana`, `chocolate`, `lemon`, `strawberry` and `vanilla`.
34+
Cho phép Lặp Lại: chẳng hạn như các đồng xu trong túi của bạn `(5,5,5,10,10)`
3535

36-
We can have three scoops. How many variations will there be?
36+
Hoặc cho rằng có năm hương vị kem:
37+
`chuối`, `sô-cô-la`, `chanh`, `dâu` và `vanilla`.
3738

38-
Let's use letters for the flavours: `{b, c, l, s, v}`.
39-
Example selections include:
39+
Chúng tôi có thể chọn ba ph��n. Sẽ có bao nhiêu biến thể?
4040

41-
- `{c, c, c}` (3 scoops of chocolate)
42-
- `{b, l, v}` (one each of banana, lemon and vanilla)
43-
- `{b, v, v}` (one of banana, two of vanilla)
41+
Hãy sử dụng các chữ cái để đại diện cho các hương vị: `{b, c, l, s, v}`.
42+
Các lựa chọn ví dụ bao gồm:
4443

45-
**Number of combinations**
44+
- `{c, c, c}` (3 phần kem sô-cô-la)
45+
- `{b, l, v}` (mỗi loại một phần của chuối, chanh và vanilla)
46+
- `{b, v, v}` (một phần của chuối, hai phần của vanilla)
4647

47-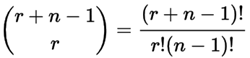
![Formula](https://www.mathsisfun.com/combinatorics/images/combinations-repeat.gif)
48+
**Số lượng tổ hợp**
4849

49-
Where `n` is the number of things to choose from, and we
50-
choose `r` of them. Repetition allowed,
51-
order doesn't matter.
50+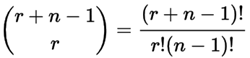
![Công thức](https://www.mathsisfun.com/combinatorics/images/combinations-repeat.gif)
5251

53-
## Cheatsheet
52+
Trong đó `n` là số lượng thứ để chọn từ, và chúng ta
53+
chọn `r` trong số đó. Cho phép lặp lại,
54+
thứ tự không quan trọng.
5455

55-
![Permutations and Combinations Overview](./images/overview.png)
56+
## Bảng Tóm Tắt
5657

57-
![Combinations overview](./images/combinations-overview.jpg)
58+
![Tổng quan về Hoán vị và Tổ hợp](./images/overview.png)
5859

59-
| | |
60-
| --- | --- |
61-
|![Combinations with repetition](./images/combinations-with-repetitions.jpg) | ![Combinations without repetition](./images/combinations-without-repetitions.jpg) |
60+
![Tổng quan về Tổ hợp](./images/combinations-overview.jpg)
6261

63-
*Made with [okso.app](https://okso.app)*
62+
| | |
63+
| ---------------------------------------------------------------- | ---------------------------------------------------------------------- |
64+
| ![Tổ hợp có lặp lại](./images/combinations-with-repetitions.jpg) | ![Tổ hợp không lặp lại](./images/combinations-without-repetitions.jpg) |
6465

65-
## References
66+
_Tạo với [okso.app](https://okso.app)_
67+
68+
## Tài liệu tham khảo
6669

6770
- [Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
68-
- [Permutations/combinations cheat sheets](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)
71+
- [Bảng Tóm Tắt Hoán vị/tổ hợp](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)

‎src/algorithms/sets/fisher-yates/README.en-EN.md

+16
Original file line numberDiff line numberDiff line change
@@ -1,2 +1,18 @@
1+
# Fisher–Yates shuffle
2+
13
_Read this in other languages:_
24
[_Tiếng Việt_](README.md)
5+
6+
The Fisher–Yates shuffle is an algorithm for generating a random
7+
permutation of a finite sequence—in plain terms, the algorithm
8+
shuffles the sequence. The algorithm effectively puts all the
9+
elements into a hat; it continually determines the next element
10+
by randomly drawing an element from the hat until no elements
11+
remain. The algorithm produces an unbiased permutation: every
12+
permutation is equally likely. The modern version of the
13+
algorithm is efficient: it takes time proportional to the
14+
number of items being shuffled and shuffles them in place.
15+
16+
## References
17+
18+
[Wikipedia](https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle)

0 commit comments

Comments
 (0)